BIP: 98 source
Layer: Consensus (soft fork)
Title: Fast Merkle Trees
Authors: Mark Friedenbach <mark@friedenbach.org>
Kalle Alm <kalle.alm@gmail.com>
BtcDrak <btcdrak@gmail.com>
Status: Draft
Type: Specification
Assigned: 2017-08-24
License: CC-BY-SA-4.0
License-Code: MIT
In many applications it is useful to prove membership of a data element in a set without having to reveal the entire contents of that set. The Merkle hash-tree, where inner/non-leaf nodes are labeled with the hash of the labels or values of its children, is a cryptographic tool that achieves this goal. Bitcoin uses a Merkle hash-tree construct for committing the transactions of a block into the block header. This particular design, created by Satoshi, suffers from a serious flaw related to duplicate entries documented in the National Vulnerability Database as CVE-2012-2459[1], and also suffers from less than optimal performance due to unnecessary double-hashing.
This Bitcoin Improvement Proposal describes a more efficient Merkle hash-tree construct that is not vulnerable to CVE-2012-2459 and achieves an approximate 55% decrease in hash-tree construction and validation times as compared with fully optimized implementations of the Satoshi Merkle hash-tree construct.
This BIP is licensed under a Creative Commons Attribution-ShareAlike license. All provided source code is licensed under the MIT license.
A Merkle hash-tree is a directed acyclic graph data structure where all non-terminal nodes are labeled with the hash of combined labels or values of the node(s) it is connected to. Bitcoin uses a unique Merkle hash-tree construct invented by Satoshi for calculating the block header commitment to the list of transactions in a block. While it would be convenient for new applications to make use of this same data structure so as to share implementation and maintenance costs, there are three principal drawbacks to reuse.
First, Satoshi's Merkle hash-tree has a serious vulnerability[1] related to duplicate tree entries that can cause bugs in protocols that use it. While it is possible to secure protocols and implementations against exploit of this flaw, it requires foresight and it is a bit more tricky to design secure protocols that work around this vulnerability. Designers of new protocols ought avoid using the Satoshi Merkle hash-tree construct where at all possible in order to responsibly decrease the likelihood of downstream bugs in naïve implementations.
Second, Satoshi's Merkle hash-tree performs an unnecessary number of cryptographic hash function compression rounds, resulting in construction and validation times that are approximately three (3) times more computation than is strictly necessary in a naïve implementation, or 2.32x more computation in an implementation specialized for this purpose only[2]. New implementations that do not require backwards compatibility ought to consider hash-tree implementations that do not carry this unnecessary performance hit.
Third, Satoshi's algorithm presumes construction of a tree index from an ordered list, and therefore is designed to support balanced trees with a uniform path length from root to leaf for all elements in the tree. Many applications, on the other hand, benefit from having unbalanced trees, particularly if the shorter path is more likely to be used. While it is possible to make a few elements of a Satoshi hash-tree have shorter paths than the others, the tricks for doing so are dependent on the size of the tree and not very flexible.
Together these three reasons provide justification for specifying a standard Merkle hash-tree structure for use in new protocols that fixes these issues. This BIP describes such a structure, and provides an example implementation.
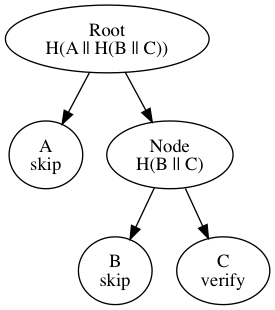
A Merkle hash-tree as defined by this BIP is an arbitrarily-balanced binary tree whose terminal/leaf nodes are labelled with the double-SHA256 hashes of data, whose format is outside the scope of this BIP, and inner nodes with labels constructed from the fast-SHA256 hash of its children's labels. The following image depicts an example unbalanced hash-tree:
A, B, and C are leaf labels, 32-byte double-SHA256 hashes of the data associated with the leaf. Node and Root are inner nodes, whose labels are fast-SHA256 (defined below) hashes of their respective children's labels. Node is labelled with the fast-SHA256 hash of the concatenation of B and C. Root is labelled with the fast-SHA256 hash of the concatenation of A and Node, and is the Merkle root of the tree. Nodes with single children are not allowed.The double-SHA256 cryptographic hash function takes an arbitrary-length data as input and produces a 32-byte hash by running the data through the SHA-256 hash function as specified in FIPS 180-4[3], and then running the same hash function again on the 32-byte result, as a protection against length-extension attacks.
The fast-SHA256 cryptographic hash function takes two 32-byte hash values, concatenates these to produce a 64-byte buffer, and applies a single run of the SHA-256 hash function with a custom 'initialization vector' (IV) and without message padding. The result is a 32-byte 'midstate' which is the combined hash value and the label of the inner node. The changed IV protects against path-length extension attacks (grinding to interpret a hash as both an inner node and a leaf). fast-SHA256 is only defined for two 32-byte inputs. The custom IV is the intermediate hash value generated after performing a standard SHA-256 of the following hex-encoded bytes and extracting the midstate:
cbbb9d5dc1059ed8 e7730eaff25e24a3 f367f2fc266a0373 fe7a4d34486d08ae
d41670a136851f32 663914b66b4b3c23 1b9e3d7740a60887 63c11d86d446cb1c
This data is the first 512 fractional bits of the square root of 23, the 9th prime number. The resulting midstate is used as IV for the fast-SHA256 cryptographic hash function:
static unsigned char _MidstateIV[32] =
{ 0x89, 0xcc, 0x59, 0xc6, 0xf7, 0xce, 0x43, 0xfc,
0xf6, 0x12, 0x67, 0x0e, 0x78, 0xe9, 0x36, 0x2e,
0x76, 0x8f, 0xd2, 0xc9, 0x18, 0xbd, 0x42, 0xed,
0x0e, 0x0b, 0x9f, 0x79, 0xee, 0xf6, 0x8a, 0x24 };
As fast-SHA256 is only defined for two (2) 32-byte hash inputs, there are necessarily two special cases: an empty Merkle tree is not allowed, nor is any root hash defined for such a "tree"; and a Merkle tree with a single value has a root hash label equal to that self-same value of the leaf branch, the only node in the tree (a passthrough operation with no hashing).
The fast-SHA256 hash function can be calculated 2.32x faster than a specialized double-SHA256 implementation[2], or three (3) times faster than an implementation applying a generic SHA-256 primitive twice, as hashing 64 bytes of data with SHA-256 as specified by FIPS 180-4[3] takes two compression runs (because of message padding) and then a third compression run for the double-SHA256 construction. Validating a fast-SHA256 Merkle root is therefore more than twice as fast as the double-SHA256 construction used by Satoshi in bitcoin. Furthermore the fastest fast-SHA256 implementation is the generic SHA-256 implementation, enabling generic circuitry and code reuse without a cost to performance.
The application of fast-SHA256 to inner node label updates is safe in this limited domain because the inputs are hash values and fixed in number and in length, so the sorts of attacks prevented by message padding and double-hashing do not apply.
The 'initialization vector' for fast-SHA256 is changed in order to prevent a category of attacks on higher level protocols where a partial collision can serve as both a leaf hash and as an inner node commitment to another leaf hash. The IV is computed using standard SHA-256 plus midstate extraction so as to preserve compatibility with cryptographic library interfaces that do not support custom IVs, at the cost of a 2x performance hit if neither custom IVs nor resuming from midstate are supported. The data hashed is a nothing-up-my-sleeve number that is unlikely to have a known hash preimage. The prime 23 was chosen as the leading fractional bits of the first eight (8) primes, two (2) through nineteen (19), are constants used in the setup of SHA-256 itself. Using the next prime in sequence reduces the likelihood of introducing weakness due to reuse of a constant factor.
The Merkle root hash of a single element tree is a simple pass-through of the leaf hash without modification so as to allow for chained validation of split proofs. This is particularly useful when the validation environment constrains proof sizes, such as push limits in Bitcoin script. Chained validation allows a verifier to split one proof into two or more, where the leaf is shown to be under an inner node, and that inner node is shown to be under the root. Without pass-through hashing in a single-element tree, use of chained validation would unnecessarily introduce a minimum path length requirement equal to the number of chain links. Pass-through hashing of single elements allows instead for one or more of the chained validations to use a "NOP" proof consisting of a zero-length path, thereby allowing, for example, a fixed series of four (4) chained validations to verify a length three (3) or shorter path.
An important use of Merkle hash-trees is the ability to compactly prove membership with log-sized proofs. This section specifies a standard encoding for a multi-element inclusion proof.
To prove that a set of hashes is contained within a Merkle tree with a given root requires four pieces of information:
- The root hash of the Merkle tree;
- The hash values to be verified, a set usually consisting of the double-SHA256 hash of data elements, but potentially the labels of inner nodes instead, or both;
- The paths from the root to the nodes containing the values under consideration, expressed as a serialized binary tree structure; and
- The hash values of branches not taken along those paths.
Serialization begins with a variable-length integer (VarInt) used to encode N, the number of internal nodes in the proof.
Next the structure of the tree is traversed using depth-first, left-to-right, pre-order algorithm to visit each internal nodes, which are serialized using a packed 3-bit representation for the configuration of each node, consuming (3*N + 7) / 8 bytes.
Then the number skipped hashes (those included in the proof, not verified by the proof) is serialized as a variable-length integer (VarInt),
followed by the hashes themselves in the order previously traversed.
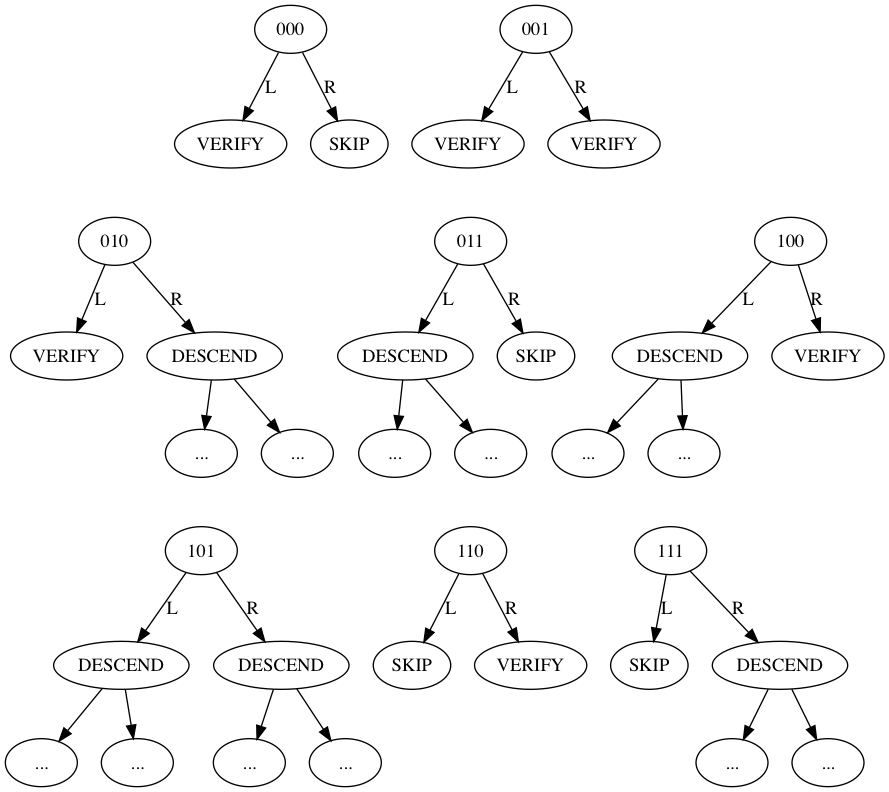
There are eight possible configurations of internal nodes, as given in the following diagram:
In this diagram, DESCEND means the branch links to another internal node, as indicated by its child graph elements labeled "..."; SKIP means the branch contains a hash of an elided subtree or element, and the fast-SHA256 root hash of this subtree or double-SHA256 hash of the element is included in the proof structure; and VERIFY means the branch contains an externally provided hash that is needed as witness for the verification of the proof. In tabular form, these code values are:| Code | Left | Right |
| 000 | VERIFY | SKIP |
| 001 | VERIFY | VERIFY |
| 010 | VERIFY | DESCEND |
| 011 | DESCEND | SKIP |
| 100 | DESCEND | VERIFY |
| 101 | DESCEND | DESCEND |
| 110 | SKIP | VERIFY |
| 111 | SKIP | DESCEND |
These 3-bit codes are packed into a byte array such that eight (8) codes would fit in every three (3) bytes.
The order of filling a byte begins with the most significant bit 0x80 and ends with the least significant bit 0x01.
Unless the number of inner nodes is a multiple of eight (8), there will be excess low-order bits in the final byte of serialization.
These excess bits must be zero.
Note that the tree serialization is self-segmenting. By tracking tree structure a proof reader will know when the parser has reached the last internal node. The number of inner nodes serialized in the proof MUST equal the number of nodes inferred from the tree structure itself. Similarly, the number of SKIP hashes can also be inferred from the tree structure as serialized, and MUST equal the number of hashes provided within the proof.
The single-hash proof has N=0 (the number of inner nodes), the tree structure is not serialized (as there are no inner nodes), and the number of SKIP hashes can be either 0 or 1.
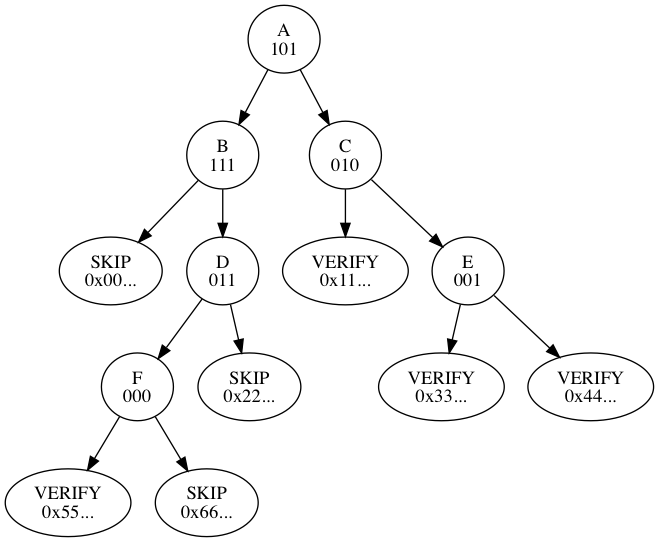
Consider the following Merkle tree structure:
There are six (6) internal nodes. The depth-first, left-to-right, pre-order traversal of the tree visits these nodes in the following order: A, B, D, F, C, then E. There are three (3) skipped hashes, visited in the following order: 0x00..., 0x66..., and 0x22... The remaining four (4) hashes are provided at runtime to be verified by the proof.| Byte 1 | Byte 2 | Byte 3 | |
| Bits | 76543210 | 76543210 | 76543210 |
| Nodes | AAABBBDD | DFFFCCCE | EE------ |
| Code | 10111101 | 10000100 | 01000000 |
The serialization begins with the VarInt encoded number of inner nodes, 0x06, followed by the tree serialization itself, 0xbd8440.
Next the number of SKIP hashes is VarInt encoded, 0x03, followed by the three (3) hashes in sequence.
The resulting 101 byte proof, encoded in base64:.
Br2EQAMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAGZmZmZmZmZmZmZmZmZmZmZmZmZm
ZmZmZmZmZmZmZmZmREREREREREREREREREREREREREREREREREREREREREQ=
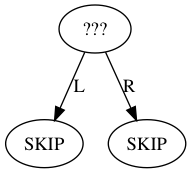
The 3-bit encoding for inner nodes allows encoding all relevant configurations of the nodes where the left and right branches can each be one of {DESCEND, SKIP, VERIFY}. The excluded 9th possibility would have both branches as SKIP:
This possibility is not allowed as for verification purposes it is entirely equivalent to the shorter proof where the branch to that node was SKIP'ed. Disallowing a node with two SKIP branches eliminates what would otherwise be a source of proof malleability.The number of hashing operations required to verify a proof is one less than the number of hashes (SKIP and VERIFY combined), and is exactly equal to the number of inner nodes serialized as the beginning of the proof as N. The variable-length integer encoding has the property that serialized integers, sorted lexicographically, will also be sorted numerically. Since the first serialized item is the number of inner nodes, sorting proofs lexicographically has the effect of sorting the proofs by the amount of work required to verify.
The number of hashes required as input for verification of a proof is N+1 minus the number of SKIP hashes, and can be quickly calculated without parsing the tree structure.
The coding and packing rules for the serialized tree structure were also chosen to make lexicographical comparison useful (or at least not meaningless). If we consider a fully-expanded tree (no SKIP hashes, all VERIFY) to be encoding a list of elements in the order traversed depth-first from left-to-right, then we can extract proofs for subsets of the list by SKIP'ing the hashes of missing values and recursively pruning any resulting SKIP,SKIP nodes. Lexicographically comparing the resulting serialized tree structures is the same as lexicographically comparing lists of indices from the original list verified by the derived proof.
Because the number of inner nodes and the number of SKIP hashes is extractible from the tree structure, both variable-length integers in the proof are redundant and could have been omitted. However that would require either construction and storage of the explicit tree in memory at deserialization time, or duplication of the relatively complicated tree parsing code in both the serialization and verification methods. For that reason (as well as to handle the single-hash edge case) the redundant inner node and SKIP hash counts are made explicit in the serialization, and the two values must match what is inferred from the tree structure for a proof to be valid. This makes deserialization trivial and defers tree construction until verification time, which has the additional benefit of enabling log-space verification algorithms.
Many applications use a Merkle tree to provide indexing of, or compact membership proofs about the elements in a list. This addendum specifies an algorithm that constructs a canonical balanced tree structure for lists of various lengths. It differs in a subtle but important way from the algorithm used by Satoshi so as to structurally prevent the vulnerability described in [1].
- Begin with a list of arbitrary data strings.
- Pre-process the list by replacing each element with its double-SHA256 hash.
- If the list is empty, return the zero hash.
- While the list has 2 or more elements,
- Pass through the list combining adjacent entries with the fast-SHA256 hash. If the list has an odd number of elements, leave the last element as-is (this fixes [1]). This step reduces a list of N elements to ceil(N/2) entries.
- The last remaining item in the list is the Merkle root.
An implementation of this BIP for extraction of Merkle branches and fast, log-space Merkle branch validation is available at the following Github repository:
https://github.com/maaku/bitcoin/tree/fast-merkle-tree
Also included in this repo is a 'merklebranch' RPC for calculating root values and extracting inclusion proofs for both arbitrary trees and trees constructed from lists of values using the algorithm in this BIP, and a 'mergemerklebranch' RPC for unifying two or more fast Merkle tree inclusion proofs--replacing SKIP hashes in one proof with a subtree extracted from another.
This BIP is used by BIP116 (MERKLEBRANCHVERIFY)[4] to add Merkle inclusion proof verification to script by means of a soft-fork NOP expansion opcode. Deployment of MERKLEBRANCHVERIFY would make the contents of this BIP consensus critical. The deployment plan for BIP116 is covered in the text of that BIP.
This BIP on its own does not cause any backwards incompatibility.
[1] National Vulnerability Database: CVE-2012-2459
[2] github.com:sipa/bitcoin 201709_dsha256_64 Pieter Wuille, September 2017, personal communication. By making use of knowledge that the inputs at each stage are fixed length, Mr. Wuille was able to achieve a 22.7% reduction in the time it takes to compute the double-SHA256 hash of 64 bytes of data, the hash aggregation function of the Satoshi Merkle tree construction.